Uncovering the power of compounding: how it can boost your investment returns

To understand what is compounding, instead of starting with the theory, let's start with a picture. Imagine that you invested $10,000 for 30 years at 5% interest rate, in one case with compounding and in another without. You can see the result in the chart below:

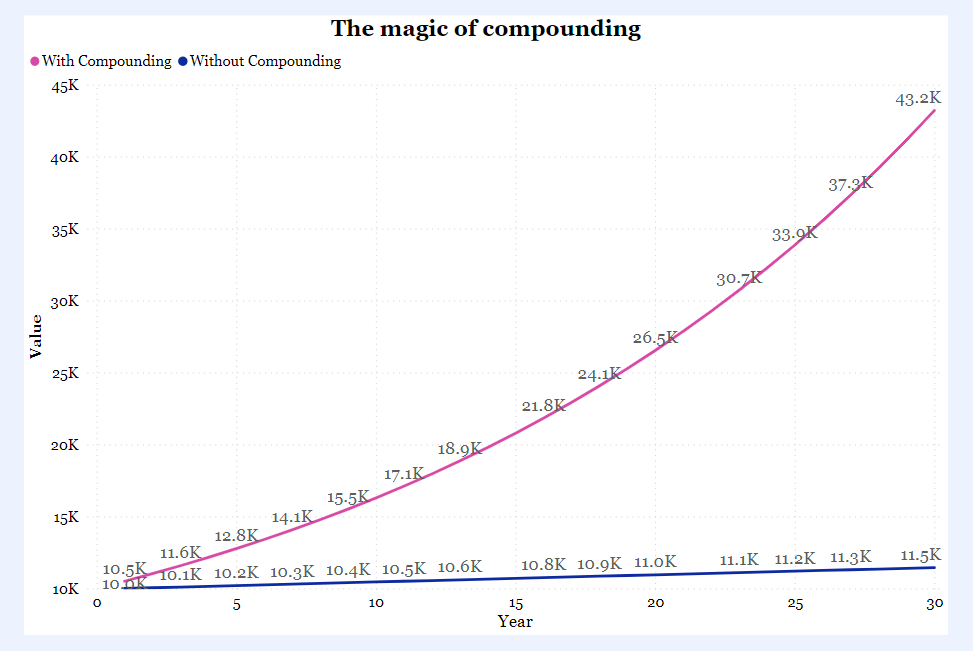
The difference is $31,769.42! Imagine how much that would be if you added money regularly!

Ok but what is compounding?! Let me explain.

Time value of money

The core financial concept behind compounding is called time value of money (TVM). It is pretty simple, and the idea is that that money available at the present time is worth more than the same amount in the future - due to its potential earning capacity.

In order to calculate how much your money will be worth in X years once invested, you can use a formula to calculate the Future Value:

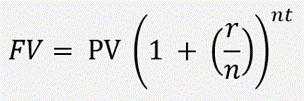
Where:

• FV = Future value of money (how much your investment will be worth)
• PV = Present value of money (how much you are investing today)
• r = interest rate
• t = number of years
• n = number of compounding periods per year.

For example, assume a sum of $10,000 is invested for one year at 10% interest. The future value of that money is:

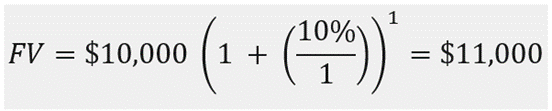
The magic of compounding

Playing with the formula above, you can simulate many cases but in this post I want to focus on the concept of compounding itself, aka the best thing invested after sliced bread.

In simple terms, compounding is the process where the value of an investment increases because you earn interest not just on the initial capital, but on the interest itself.

Let’s take a look at an example using the same numbers as above. Suppose a $10,000 investment in company X earns 10% the first year. Like we've seen, the total investment is then worth $11,000. Next assume that in the second year the investment earns another 10%. In year two, the total balance of $11,000 would earn 10%, ending with a value of $12,100 instead of $12,000. The extra $100 of growth is due to the $1000 earning of year one, also growing at 10% in year two, along with the original amount of money (called principal).

Compounding is often referred to as "magic" because it is one of the most fundamental ways to build wealth, yet takes the least amount of effort. Given time, earning interest on interest can exponentially grow your money behind the scenes, doubling, tripling and sometimes even quadrupling your money.

Compounding periods

An important note is the number of compounding periods (factor n in the formula above). This impacts how often the interest amount is calculated and paid. Although technically the interest is matured every second, banks and other financial institutions generally compound it (give it to you) on a monthly/semi-annual or annual basis.

The shorter the interval between interest calculations, the faster interest will accrue and vice versa. Thus, an account which calculates and pays interest on a daily basis will grow faster than the same account calculating interest on a monthly basis. Let’s look at another example.

You win the lottery and get $1,000,000. You decide that you want to invest all the money in a savings account. However, your bank has two different plans:

• Plan 1: the bank gives you a 6% interest rate and compounds the interest each month
• Plan 2: the bank gives you a 12% interest rate and compounds the interest every 2 months.

Which plan would you pick?

The example is a bit counterintuitive, didn’t we say that shorter intervals are better? Yes, but this case is a bit extreme because the interest rate of Plan 2 is double so it “neutralises” the effects of having the compounding every 2 months instead of every month (in Plan 1). But you get the idea.

How to calculate it

If you like excel and want to create some charts in your financial tracker (cause you have one, right?), the easiest formula that you can use in Excel is:

FV(rate,nper,pmt,[pv],[type])

To see more details about how to use the formula, you can check the official Microsoft guideline or the Google sheet guideline.

What if I am allergic to math and I just want a zero-effort calculator? Even in that case I got you covered! There are many tools out there but you can find a good one on this post I wrote, where you can see how your money would grow with or without recurrent monthly payments.

I hope you now understand the importance to start saving early, compounding can really do magic!